Recently, a research group led by Prof. Yong-Chun Liu from Tsinghua’s Department of Physics proposed a time crystal model in a single-mode nonlinear cavity. This work was published in Physical Review Letters under the title of "Time crystal in a single-mode nonlinear cavity".
Time crystal is an analogy of space crystal in the time dimension. As the space crystal has a periodic structure, the representative character of a time crystal is the long-time stable periodic oscillation. Interestingly, such a kind of oscillation does not originate from the intrinsic period of the system. Instead, it originates from the spontaneous breaking of the time-translation symmetry. The concept of time crystal was first proposed by Shapere and Wilczek in 2012 and attracted lots of interest from all over the world due to its breakthrough ideas, interesting properties, and potential applications. The original model of time crystal was ruled out by several subsequent studies. Then the time crystal was generalized into open quantum systems, mainly quantum many-body systems. In theory, there is an inevitable challenge when simulating or calculating the quantum many-body systems, i.e., the exponential increase of the Hilbert space dimensions. In conventional studies, mean-field approximation or cluster mean-field approximation is used to reduce the difficulty. It leads to a question that whether the time crystal phases obtained in these many-body models are pseudo-signals due to the approximations. In experiments, it is also difficult to observe time crystal phenomena through the realization of couplings between a large number of quantum systems.
This work proposed a time crystal model in a single-mode nonlinear cavity (Fig. 1), which can well solve the above problems. A single-mode nonlinear system is a zero-dimensional system. Consequently, this work can calculate the model exactly in the truncated Hilbert space and provide clear results of the time crystal phase. This work proves the emergence of purely imaginary eigenvalues of the Liouvillian operator in the thermodynamic limit. It corresponds to periodic oscillation with increasing relaxation time (Fig. 2). These results verify the existence of time crystal in this model.
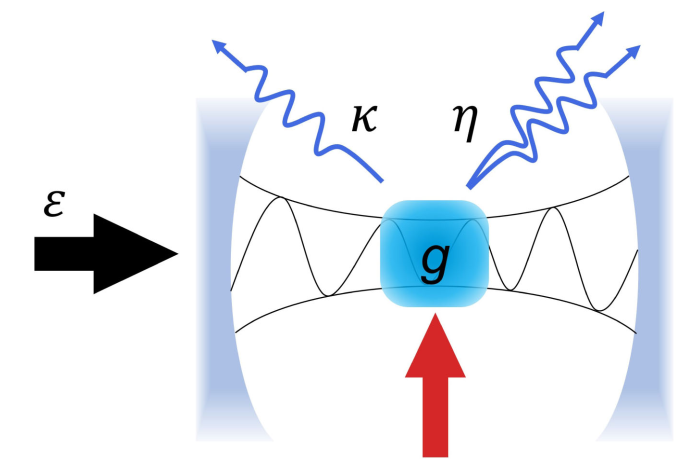
Fig. 1. Sketch of the single-mode nonlinear cavity.
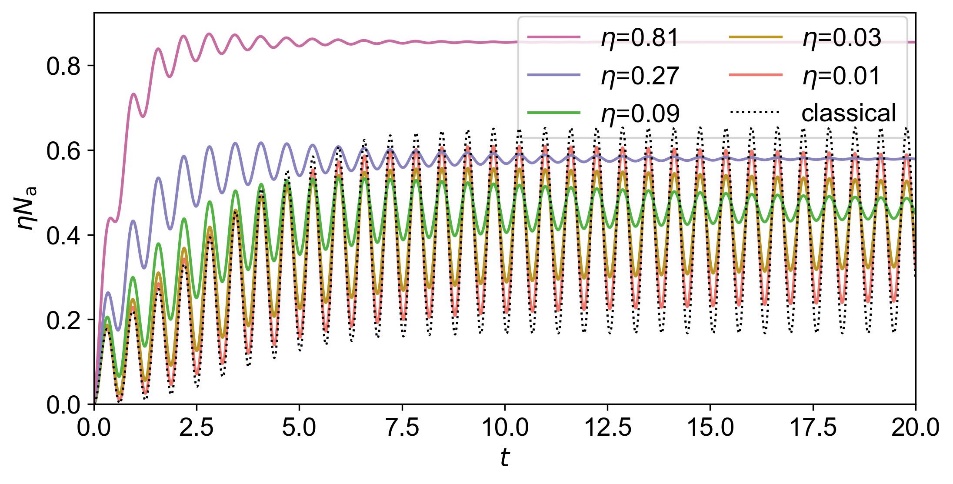
Fig. 2. The time evolution of rescaled photon number. The colored solid lines indicate the quantum results, and the black dashed line indicates the classical result.
Moreover, the authors discover a dissipative phase transition in the model, and they show the phase transition point corresponds to a Hopf bifurcation in the reduced classical model. They provide two kinds of evidences to prove the existence of dissipative phase transition. One is the closing of the dissipative gap at the phase transition point in the thermodynamic limit. The other is the first-order transition of the steady-state properties (Fig. 3), including the emergence of the quantum limit cycle and the transition of rescaled photon fluctuation. The rescaled photon fluctuation is a good order parameter to characterize the phase transition. In the equilibrium phase, this physical quantity will approach zero in the thermodynamic limit. However, in the time crystal phase, this physical quantity remains nonzero in the thermodynamic limit.
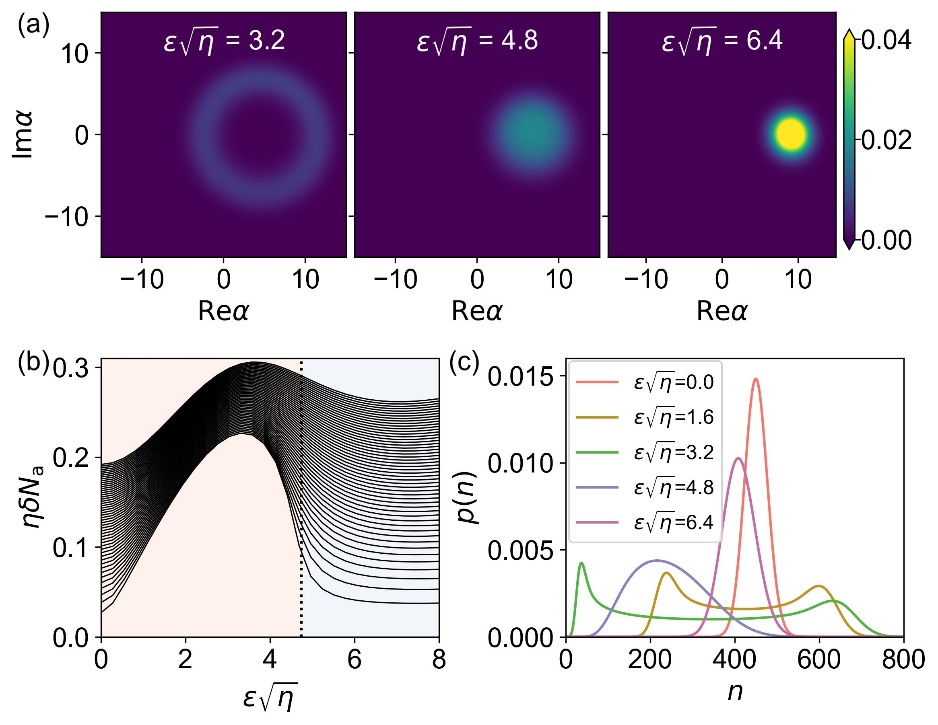
Fig. 3. Quantum limit cycle and photon statistics in the steady state. (a) Steady-state quantum Husimi distributions in the time crystal phase, critical regime, and the equilibrium phase from left to right. (b) The rescaled photon number fluctuation as a function of rescaled driving strength. It is closer to the thermodynamic limit from the bottom up. (c) The photon distributions for five different rescaled driving strengths.
The corresponding author of the paper is associate professor Yong-Chun Liu, the first author of the paper is graduate student Yaohua Li, and the collaborators of the paper include graduate student Chenyang Wang and Yuanjiang Tang. All of the authors are from the Department of Physics, Tsinghua University.
Research link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.183803
Editor: Li Han

